*Algorithms*

Hidden Markov Model, is being used for solving temporal probabilistic reasoning!

This model is one that observes the sequence of emission but was unaware of this fact that sequence of a state that required to generate the emissions. After analyzing this model it seeks to recover the sequence state from the observed data.

Letting you know the example, considering the Markov Model with two states along with six possible emissions. Thus, the model uses:

• A Red Die, which has six sides and is labeled 1 through 6
• A Green Die, which has 12 sides out of which 5 are labeled 2 through 6, while the rest 7 sides are labeled as 1
• A weighted Red Coin, for which the probability of getting HEAD is .9 and the probability of getting TAIL is .1
• A weighted Green Coin, for which the probability of getting HEAD is .95 and the probability of getting TAIL is .05
• Now, the model creates the sequence of numbers set {1, 2, 3, 4, 5, 6} following the given guidelines:
• Start off with the roll- off the Red Die, record the outcome along with its emission
• Toss the Red Coin and observe the following:

                Case 1: Outcome is HEAD, roll the Red Die and record the observation

                Case 2: Outcome is TAIL, roll the Green Die and record the observation

• At every step, you keep on flipping the coin in shade equivalence roll the same die as in the previously mentioned step. The rolling of the die should be same to what is mentioned above

The state diagram of this model has 2 states that are RED or GREEN, as in the figure given below:

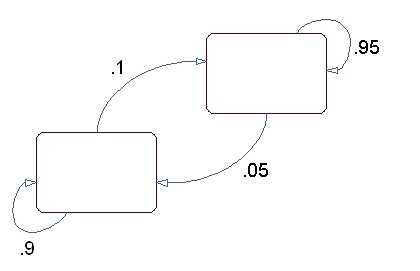
You decide the discharge from a state by rolling the die with an indistinguishable color from the state. You decide the progress to the following state by flipping the coin with an indistinguishable color from the state.  

The Transition Lattice is:  

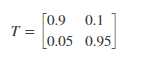
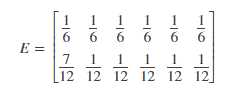
The Emission Lattice is:

The model isn't concealed in light of the fact that you know the arrangement of states from the shades of the coins and dice. Assume, in any case, that another person is producing the emanations without demonstrating to you the dice or the coins. All you see is the succession of emanations. In the event that you begin seeing more 1s than different numbers, you may presume that the model is in the green state, however, you can't make sure in light of the fact that you can't see the shade of the bite the dust being rolled.

Here, we come to an end of the discussion about the Hidden Markov Model!

Cheers!